Test de Logique
Défi Mathématiques du mercredi 27 septembre 2023
Delphine D. / Le Palais des Echecs
Bienvenue sur mon blog dédié aux jeux d'échecs, l'univers fascinant où stratégie et créativité se rencontrent sur un échiquier. Je suis passionné par ce jeu depuis mon plus jeune âge et je suis ravi de partager avec vous ma passion pour les échecs. En tant que fervent joueur, je suis constamment à la recherche de nouvelles ouvertures, de combinaisons audacieuses et de finales inspirantes. J'aime explorer les multiples facettes de ce jeu millénaire, en étudiant les grands maîtres et en analysant leurs parties historiques. Mais ce blog ne se limite pas aux conseils et aux analyses. Je souhaite également créer une communauté engagée de joueurs d'échecs qui partagent leur enthousiasme et leur expérience. Nous pourrons discuter des dernières nouveautés, des tournois à venir, des techniques d'apprentissage et même des anecdotes liées à nos propres parties. Rejoignez-moi dans cette aventure où chaque coup est un pas vers la victoire, et où chaque défaite nous offre une occasion d'apprendre. Les échecs sont bien plus qu'un simple jeu pour moi, c'est une passion qui nous unit tous. En Savoir plus sur Delphine D. Rédactrice spécialisée - Facebook - Pinterest - Youtube

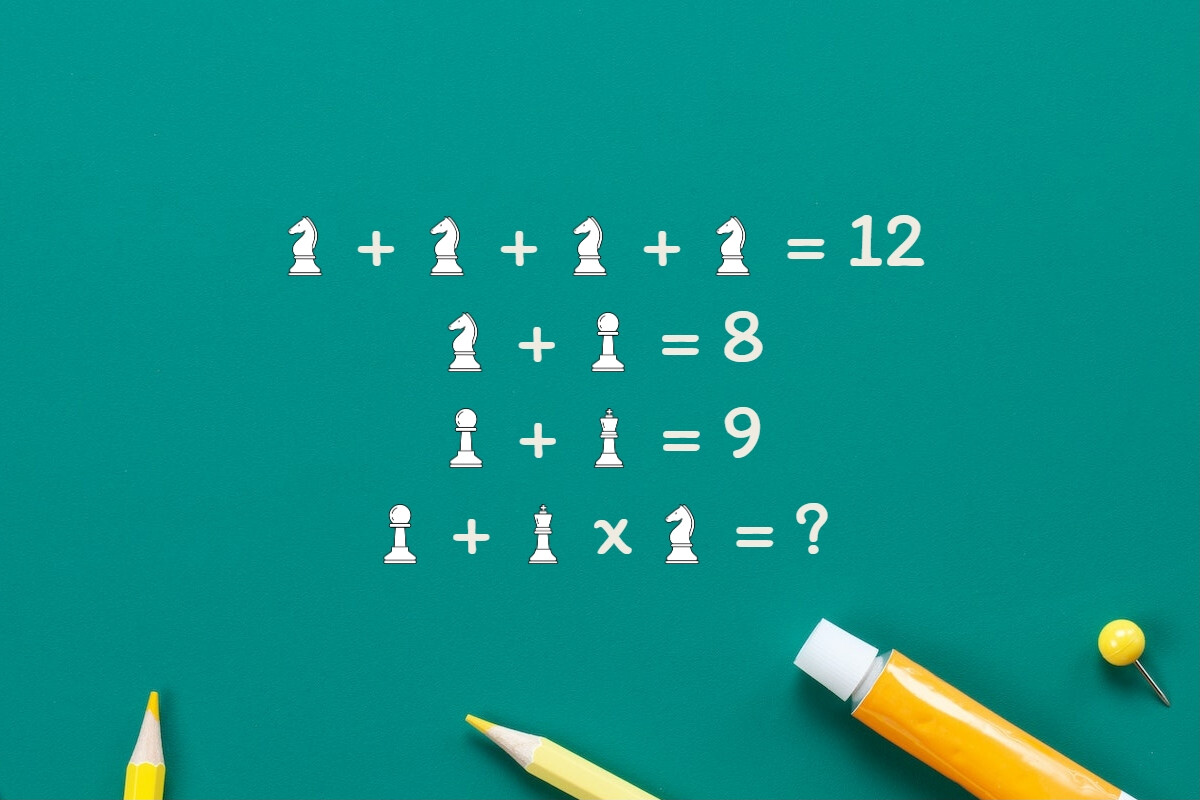
Faut-il vraiment être intelligent pour jouer aux échecs?
Les échecs, un jeu de stratégie vieux de plusieurs siècles, est souvent associé à l’intelligence, [...]
Défi Mathématiques du mardi 19 septembre 2023
...
Echec et Mat en 2 Coups du samedi 26 août 2023
[post_chess csv=’puzzle_2′][affiche_puzzle][affiche_puzzle_result]