Test de Logique
Défi Mathématiques du mardi 26 septembre 2023
Système d'équations avec les icônes cavalier, pion et reine
Bienvenue sur notre site internet qui présente un système de 4 équations avec des inconnues représentées par les icônes
 (cavalier),
(cavalier),
 (pion) et
(pion) et

Nous devons trouver les valeurs de cavalier, pion, reine et également la valeur de la quatrième équation, représentée par un '?'.
Les équations du système sont les suivantes :
- Équation 1 : 1 * x = 2
- Équation 2 : 1 * x + 3 * y = 17
- Équation 3 : y + 1 * (1 * z) = 9
- Équation 4 : y + z * 3 * x = ?
Pour résoudre ce système d'équations, nous allons remplacer les valeurs de chaque inconnue par le nom des icônes correspondantes. Ainsi, nous remplaçons :
- x par 'cavalier'
- y par 'pion'
- z par 'reine'
La solution que nous devons trouver est le résultat de l'équation 'y + z * 3 * x = ?', que nous appellerons 'w'.
Commençons par résoudre l'équation 1 : 1 * x = 2
En remplaçant x par 'cavalier', l'équation devient : 1 * 'cavalier' = 2
Divisons des deux côtés par 1 pour isoler 'cavalier' :
'cavalier' = 2
Passons maintenant à l'équation 2 : 1 * x + 3 * y = 17
En remplaçant x par 'cavalier' et y par 'pion', l'équation devient : 1 * 'cavalier' + 3 * 'pion' = 17
Isolons 'pion' en soustrayant 3 * 'cavalier' des deux côtés :
3 * 'pion' = 17 - 1 * 'cavalier'
Divisons des deux côtés par 3 pour obtenir la valeur de 'pion' :
'pion' = (17 - 1 * 'cavalier') / 3
Continuons avec l'équation 3 : y + 1 * (1 * z) = 9
En remplaçant y par 'pion' et z par 'reine', l'équation devient : 'pion' + 1 * (1 * 'reine') = 9
Isolons 'reine' en soustrayant 'pion' des deux côtés :
'reine' = 9 - 'pion'
Enfin, résolvons l'équation 4 : y + z * 3 * x = ?
En remplaçant y par 'pion', z par 'reine' et x par 'cavalier', l'équation devient : 'pion' + 'reine' * 3 * 'cavalier' = ?
Notons que nous devons trouver la valeur de '?' que nous appellerons 'w'.
Félicitations, nous avons maintenant toutes les valeurs nécessaires pour résoudre le système d'équations !
Évaluation des compétences
 29
29




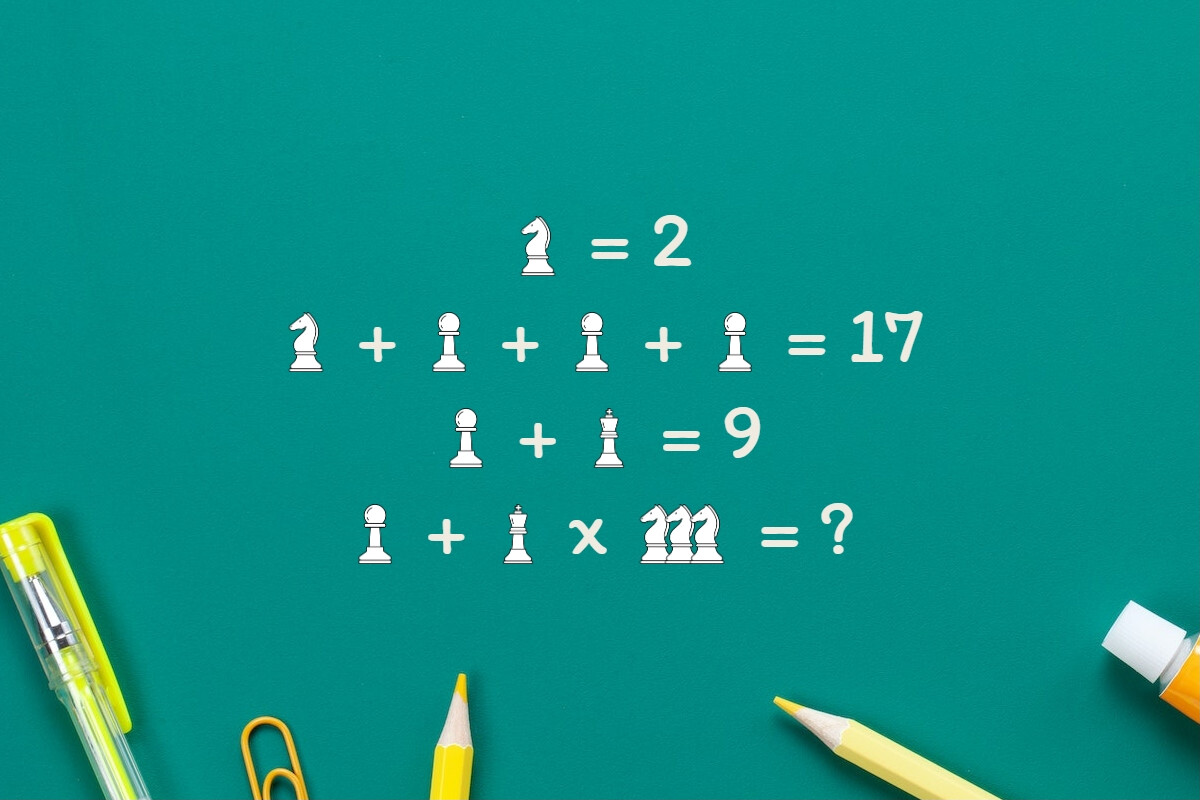
Défi Mathématiques du mercredi 27 septembre 2023
...
Les 3 meilleurs films sur les échecs
Les échecs représentent une distraction d’un particulier charme. Ils sont même de plus en plus [...]
Défi Echec et Mat en 2 Coups du samedi 30 septembre 2023
Echecs en 2 coups : Cherubino Staldi vs Uulberg, Munich, 1936La partie d'échecs entre Cherub...