Test de Logique
Défi Mathématiques du vendredi 22 septembre 2023
Système d'équations avec des icônes
Bienvenue sur notre site internet où nous présentons un système de 4 équations avec les inconnues sous forme d'icônes : le cavalier, le pion et la reine. Nous allons traduire les noms de chaque icône en français : cavalier, pion et reine.
Le but est de trouver la valeur du cavalier, du pion, de la reine et enfin la valeur de la quatrième équation. Nous allons maintenant présenter les équations :
- Première équation : 1*x = 1
- Deuxième équation : 2*x + 1*y = 7
- Troisième équation : y + 2*(3*z) = 29
- Quatrième équation : y + z*1*x = ? (représentée par un '?')
Pour expliquer la résolution de ce système d'équations, nous allons remplacer les valeurs des équations par le nom des icônes. Nous utiliserons donc le nom 'cavalier' pour 'x', 'pion' pour 'y' et 'reine' pour 'z'.
La solution que nous devons trouver est le résultat de l'équation 'y + z*1*x = ?' que nous appellerons 'w'.
Lorsque nous mentionnerons un picto dans le texte, nous l'illustrerons avec la balise <img> de la manière suivante :
pour 'cavalier' et 'x'
pour 'pion' et 'y'
pour 'reine' et 'z'
Nous n'utiliserons pas plusieurs fois les icônes pour éviter la confusion.
Nous allons maintenant expliquer comment résoudre cette équation point par point :
1. Première équation : 1*cavalier = 1
Comme la multiplication par 1 ne change pas la valeur, nous avons 'cavalier = 1'.
2. Deuxième équation : 2*cavalier + 1*pion = 7
En utilisant la valeur de 'cavalier' trouvée précédemment, nous avons '2*1 + 1*pion = 7'. En simplifiant, nous obtenons '2 + pion = 7', donc 'pion = 7 - 2' et 'pion = 5'.
3. Troisième équation : pion + 2*(3*reine) = 29
En utilisant les valeurs de 'pion' et 'reine' trouvées précédemment, nous avons '5 + 2*(3*z) = 29'. En simplifiant, nous obtenons '5 + 6*z = 29', donc '6*z = 24' et 'z = 4'.
4. Quatrième équation : pion + z*1*cavalier = ?
En utilisant les valeurs de 'pion', 'z' et 'cavalier' trouvées précédemment, nous avons '5 + 4*1*1 = ?'. En simplifiant, nous obtenons '5 + 4 = ?', donc '9 = ?'. La solution est donc 'w = 9'.
La solution de la dernière équation est donc 'w = 9', représentée par un '?'.
En résolvant ce système d'équations,


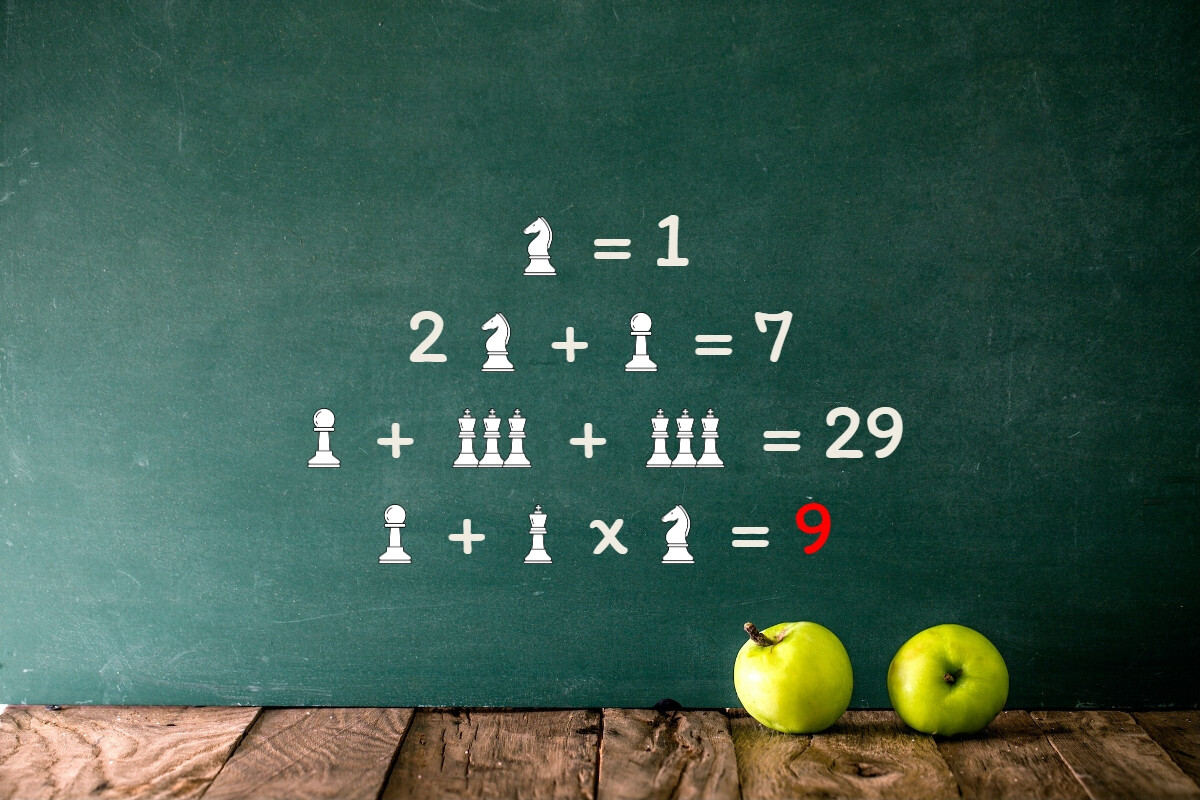

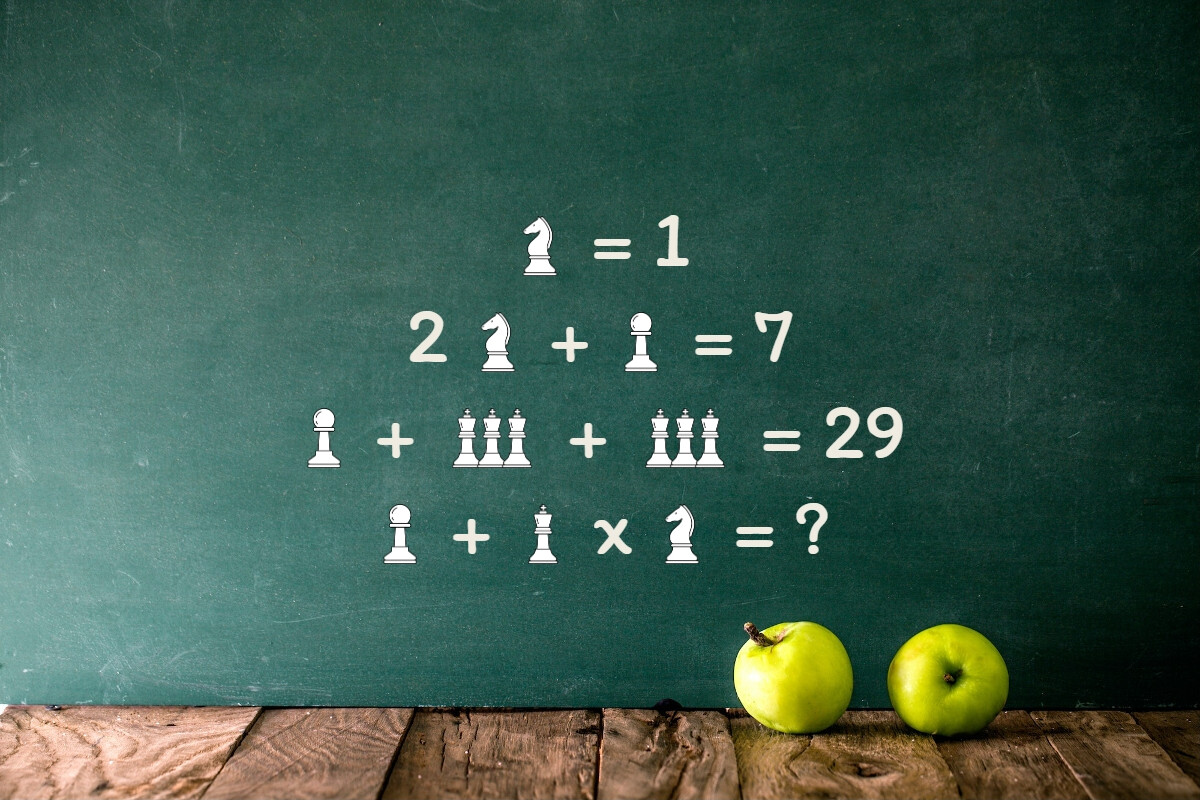
 pour 'cavalier' et 'x'
pour 'cavalier' et 'x' pour 'pion' et 'y'
pour 'pion' et 'y' pour 'reine' et 'z'
pour 'reine' et 'z'
Défi Echec et Mat en 2 Coups du mardi 19 septembre 2023
Echecs en 2 coups : Albin Planinec vs Milan Matulovic, Novi Sad, 1965La partie d'échecs [...]
7 bienfaits sur votre mental que vous apporte les échecs
Chaque coup aux échecs à un but. Il a également un impact sur le résultat [...]
Alekhine conclut par un mat spectaculaire sur l’aile roi – Défi Echec et Mat en 2 Coups du 2026-02-02
Défi du Saurez-vous trouver l’échec et mat en 2 coups ? Un défi d’échecs rapide [...]