Test de Logique
Quiz de Mathématiques et de Logique du 11 Septembre
Système d’équations avec des icônes
Bienvenue sur notre site qui présente un système de 4 équations avec des inconnues représentées par des icônes : le cavalier, le pion et la reine. Dans cette page, nous allons vous expliquer comment résoudre ce système d'équations afin de trouver les valeurs du cavalier, du pion, de la reine et enfin, du résultat de la quatrième équation, représenté par un '?'.
Les icônes :
- Cavalier : représenté par l'icône d'un chevalier à cheval.
- Pion : représenté par l'icône d'un petit pion de jeu d'échecs.
- Reine : représentée par l'icône d'une reine, couronnée d'une couronne.
Les équations :
Tout d'abord, notons les 4 équations :
- 4*x = 8
- 2*x + 2*y = 6
- y + 1*(3*z) = 16
- y + z*3*x = ?
Afin de résoudre ce système d'équations, nous allons remplacer les icônes par les inconnues correspondantes :
- Le cavalier sera représenté par 'x'.
- Le pion sera représenté par 'y'.
- La reine sera représentée par 'z'.
La solution que nous cherchons est le résultat de la quatrième équation, que nous allons appeler 'w'.
L'objectif de ce test est de trouver la solution de la dernière équation le plus rapidement possible, ce qui nous permettra d'évaluer vos compétences en mathématiques et votre QI.
Maintenant, expliquons comment résoudre ce système d'équations :
Pour la première équation, nous avons :
4*x = 8
Pour trouver la valeur du cavalier (x), nous devons diviser les deux côtés de l'équation par 4 :
x = 8 / 4
x = 2
Passons ensuite à la deuxième équation :
2*x + 2*y = 6
En utilisant la valeur de x trouvée précédemment, nous pouvons résoudre cette équation :
2*2 + 2*y = 6
4 + 2*y = 6
2*y = 6 - 4
2*y = 2
y = 2 / 2
y = 1
Poursuivons avec la troisième équation :
y + 1*(3*z) = 16
Remplaçons y par sa valeur précédemment trouvée :
1 + 1*(3*z) = 16
1 + 3*z = 16
3*z = 16 - 1
3*z = 15
z = 15 / 3
z = 5
Enfin, nous pouvons résoudre la quatrième équation :
y + z*3*x = ?
Remplaçons les variables par leurs valeurs respectives :
1 + 5*3*2 = ?
1 + 30 = ?
31 = w
Ainsi, la solution de la dernière équation est 'w' = 31.
Félicitations ! Vous avez résolu avec succès ce système d'équations et trouvé la valeur du résultat.
Nous espérons que cet exercice vous a permis de




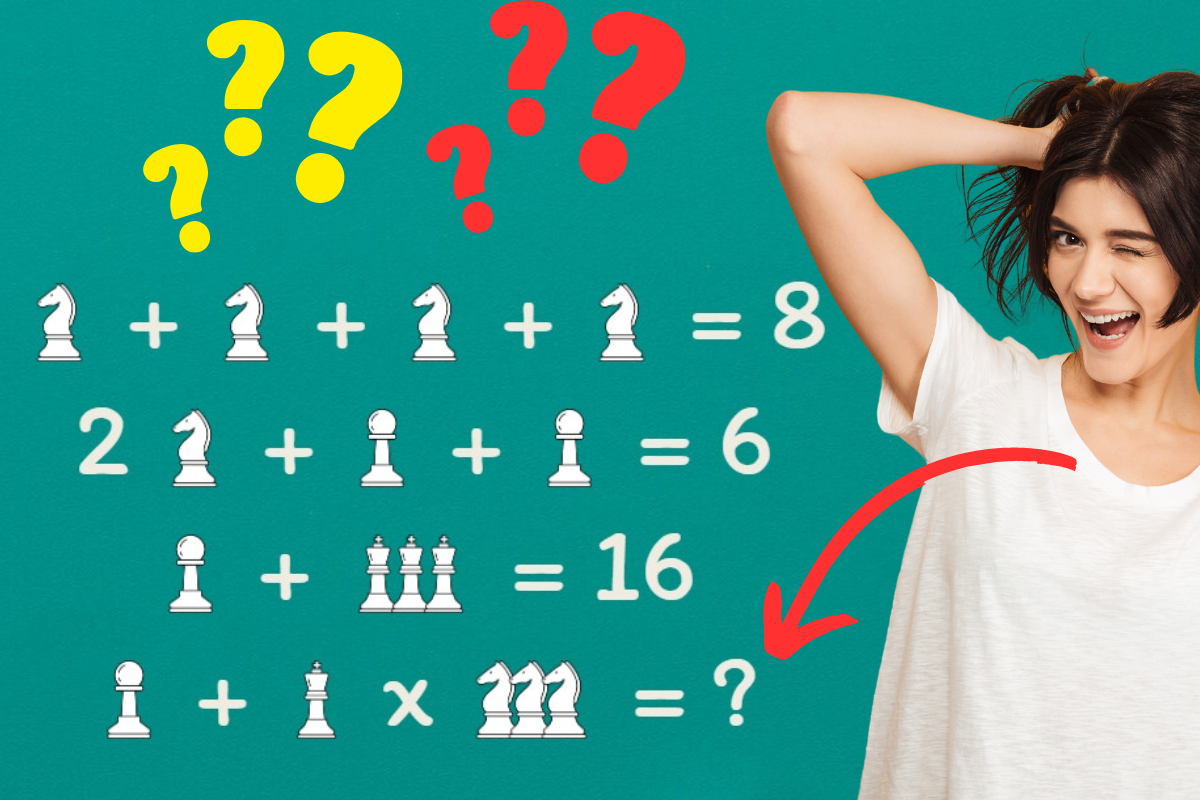
Mat spectaculaire avec la dame et la tour – Défi Echec et Mat en 2 Coups du 2026-01-27
Défi du Saurez-vous trouver l’échec et mat en 2 coups ? Un défi d’échecs rapide [...]
Défi Echec et Mat en 2 Coups du lundi 11 septembre 2023
Saurez vous résoudre cet Echec et Mat du lundi 11 septembre 2023
Défi Echec et Mat en 2 Coups du mardi 5 septembre 2023
Saurez vous résoudre cet Echec et Mat du mardi 5 septembre 2023