Test de Logique
Défi Mathématiques du jeudi 21 septembre 2023
Résolution du système d’équations avec des icônes
Sur cette page, nous présentons un système de 4 équations avec les inconnues représentées par des icônes : le cavalier, le pion et la reine. Nous devons trouver les valeurs du cavalier (x), du pion (y), de la reine (z) et du résultat de la quatrième équation (représentée par ?).
Les icônes
Pour faciliter la compréhension, voici les noms des icônes en français :
- Le cavalier
- Le pion
- La reine
Les équations
Nous devons résoudre les équations suivantes :
- 3*x = 9
- 1*x + 4*y = 11
- y + 3*(2*z) = 20
- y + z*3*x = ?
Résolution du système d’équations
Pour résoudre ce système d'équations, nous allons remplacer les valeurs des inconnues par les noms des icônes :
- La première équation devient : 3*cavalier = 9
- La deuxième équation devient : 1*cavalier + 4*pion = 11
- La troisième équation devient : pion + 3*(2*reine) = 20
- La quatrième équation reste : pion + reine*3*cavalier = ?
La solution à trouver
Nous devons trouver la valeur de la quatrième équation, représentée par un '?'. Dans cette explication, nous l'appellerons 'w'.
Résolution étape par étape
Nous allons résoudre cette équation en suivant les étapes suivantes :
- Isolons le terme avec '?': w = pion + reine*3*cavalier
- Substituons les valeurs des équations précédentes :
- w = pion + reine*3*cavalier
- w = pion + (pion + 3*(2*reine))*3*cavalier
- w = pion + (pion + 3*(2*(pion + 3*(2*reine))))*3*cavalier
- Simplifions l'expression :
- w = pion + (pion + 3*(2*(pion + 6*reine)))*3*cavalier
- w = pion + (pion + 6*(2*pion + 12*reine))*3*cavalier
- w = pion + (pion + 6*(2*pion + 12*reine))*3*cavalier
- w = pion + (pion + 12*pion + 72*reine)*3*cavalier
- w = pion + (13*pion + 72*reine)*3*cavalier
- w = pion + 39*pion*cavalier + 216*reine*cavalier
- w = (1 + 39*cavalier)*pion + 216*reine*cavalier
Conclusion
La valeur de la



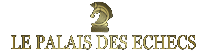




8 choses à savoir avant d’acheter une table d’échecs
Nous sommes contents que vous ayez décidé d'acheter un échiquier. C'est le signe que les [...]
Attention : 97,3% échouent à cette énigme d’allumettes ! Oserez-vous relever le défi ?
Casse-tête des allumettes Les puzzles d’allumettes sont des casse-têtes populaires qui englobent divers types, tels [...]
Défi Mathématiques du samedi 16 septembre 2023
Saurez vous ce défi mathématiques du samedi 16 septembre 2023